Circuits RLC – Théorie et Applications

📝 Exercice 1: RLC Forcé et Diagramme de Fresnel

On associe en série un condensateur de capacité \(C\), une bobine d’inductance \(L\) et un résistor de résistance \(R = 50\,\Omega\). L’ensemble est alimenté par un générateur de tension alternative de fréquence \(N\) variable : \(u(t) = U\sqrt{2}\sin(2\pi Nt)\) avec \(U = 6\,V\).

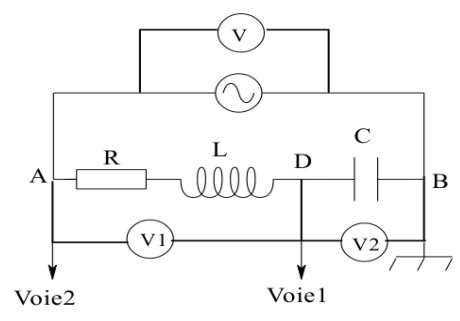
1. Quelles sont les tensions visualisées sur les voies 1 et 2 de l’oscilloscope ?
2. Pour une valeur \(N_1 = 50\,Hz\) de \(N\), les trois voltmètres indiquent la même valeur :
   1. Laquelle des deux courbes représente \(u(t)\)?
   2. Calculer le déphasage \(\Delta\varphi\) entre les deux tensions
   3. En déduire \(\varphi_u – \varphi_i\). Dire si le circuit est capacitif ou inductif
   4. Exprimer \(C\) et \(L\) en fonction de \(R\) et \(N_1\) et calculer leurs valeurs
   5. Faire, à l’échelle \(1\,cm\) représente \(2\,V\), la construction de Fresnel relative à ce circuit
   6. Établir les expressions de \(i(t)\) et de \(u_{AD}(t)\)
3. Pour une autre valeur \(N_2\) de \(N\) les deux courbes deviennent en quadrature de phase :
   
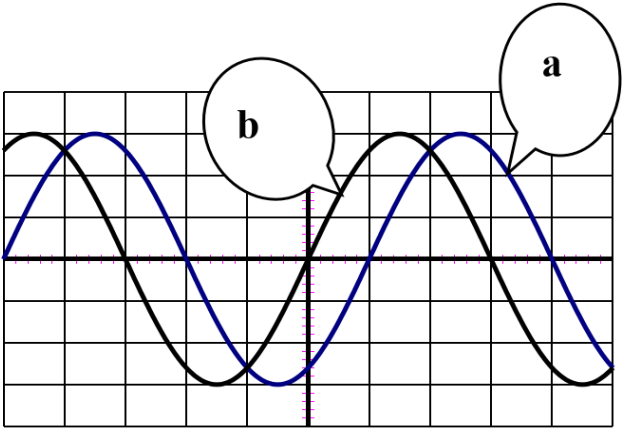
   1. Montrer que le circuit est en état de résonance d’intensité
   2. Calculer \(N_2\), \(U_c\) et \(U_{AD}\)
   3. Montrer que la tension efficace aux bornes du condensateur peut se mettre sous la forme \(U_c = Q\cdot U\), donner l’expression de \(Q\)

📝 Exercice 2: Circuit RLC en Régime Forcé

Le circuit électrique comporte en série :

• un condensateur de capacité \(C\)
• un résistor de résistance \(R = 160\,\Omega\)
• une bobine d’inductance \(L\) et de résistance propre \(r\)

L’ensemble est alimenté par un G.B.F, délivrant une tension sinusoïdale \(u(t) = 20\sqrt{2}\sin(2\pi Nt)\), de fréquence \(N\) réglable.

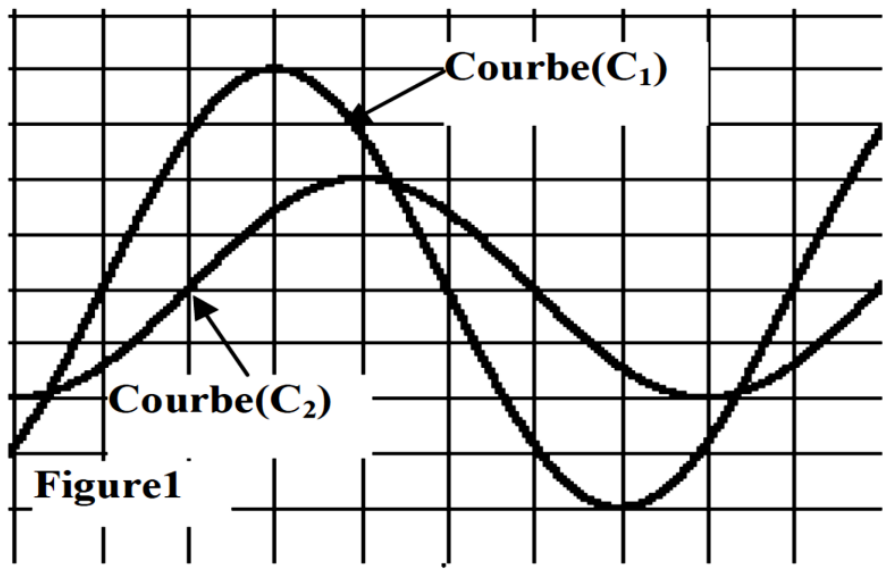
1. Montrer que la courbe de la voie (B) correspond à celle de \(u_B(t)\)
2. À l’aide d’un oscilloscope bi-courbe on visualise les tensions \(u_B(t)\) et \(u_R(t)\) respectivement aux bornes de la bobine et aux bornes du résistor. On obtient, sur l’écran de l’oscilloscope, les deux courbes suivantes :
   
   En utilisant les courbes, déterminer :
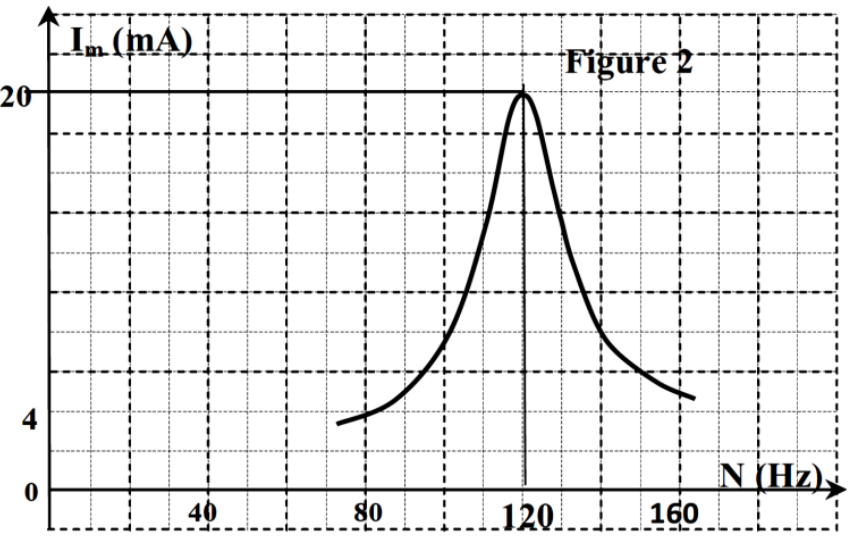
   1. La fréquence excitatrice \(N\)
   2. Les tensions maximales \(U_{Rm}\) et \(U_{Bm}\)
   3. L’impédance \(Z\) du circuit
   4. Le déphasage de la tension \(u_B(t)\) par rapport au courant \(i(t)\)
3. Construction et analyse :
   1. Faire une construction de Fresnel décrivant les oscillations du circuit où l’on représentera les vecteurs associés aux tensions \(u_R(t)\), \(u_B(t)\), \(u(t)\) et \(u_C(t)\). Échelle : \(1\,cm \rightarrow 2\sqrt{2}\,V\)
   2. Déduire les valeurs de \(r\), \(L\) et \(C\)
   3. Déterminer le déphasage de la tension \(u(t)\) par rapport à \(i(t)\). Préciser la nature du circuit
   4. Calculer la valeur de la puissance moyenne consommée par le résonateur pour cette fréquence
4. On règle la fréquence du GBF à une valeur pour laquelle la tension \(u_C(t)\) aux bornes du condensateur devient en quadrature de phase avec la tension \(u(t)\).
   1. Montrer que le circuit est siège d’une résonance d’intensité
   2. Calculer la valeur maximale \(I_{m0}\) de l’intensité de courant
   3. Calculer la puissance moyenne consommée par le circuit
   4. Dire, en le justifiant, s’il y a apparition du phénomène de surtension dans ces conditions
   5. Montrer que, dans ces conditions, \(u(t) = (R+r)\cdot i(t)\)
   6. En déduire que, dans ces conditions, l’énergie électromagnétique du circuit est conservée

📝 Exercice 3: Générateur Basses Fréquences RLC

Circuit RLC série composé de :

• un GBF : \(u(t) = U_m\sin(\omega t)\)
• un condensateur : \(C = 4,5\,\mu F\)
• un résistor : \(R = 200\,\Omega\)
• une bobine : inductance \(L\), résistance négligeable

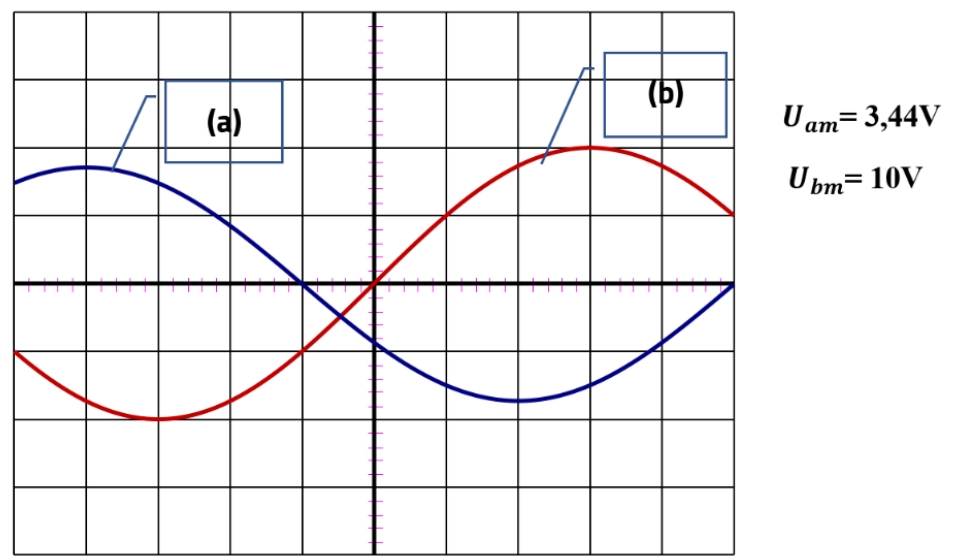
1. Vérifier que le déphasage \(|\Delta\varphi| = \frac{5\pi}{6}\,\text{rad}\)
2. Montrer que \(u_X(t)\) ne peut pas être \(u_R(t)\)
3. Analyser les courbes de l’oscilloscope :
   1. Identifier la courbe (b) comme représentant \(u(t)\)
   2. Montrer que \(\varphi_u – \varphi_i = \frac{\pi}{3}\)
   3. Déterminer la nature du circuit (inductif ou capacitif)
4. Construction de Fresnel :
   1. Réaliser la construction avec l’échelle appropriée
   2. Déduire l’expression de \(I_m\) et \(\tan(\varphi_u – \varphi_i)\)
5. Déterminer la valeur de l’inductance \(L\) de la bobine

🔄 Partie II: Étude à \(\omega = \omega_2\)

Pour une nouvelle pulsation \(\omega = \omega_2\), le voltmètre indique une tension nulle.

1. Démontrer l’état de résonance d’intensité
2. Calculer le déphasage \(\Delta\varphi = \varphi_u – \varphi_{uc}\)
3. Déterminer le coefficient \(Q\) de surtension